线性二次型最优职掌（Linear Quadratic Regulator，LQR）是一种具有二次型机能目标的最优职掌办法，用安谧性表面治理“参数优化题目”，通过选用得当的权重参数

线性二次型最优职掌（Linear Quadratic Regulator，LQR）是一种具有二次型机能目标的最优职掌办法，用安谧性表面治理“参数优化题目”，通过选用得当的权重参数，能够正在保障编制安谧的条件下，使二次型机能目标最小化，从而使编制的过渡进程具有较好的机能，所以正在试验上获得平凡利用。LQR职掌思思是通过策画最优职掌变量使得二次型标的函数最小化，精确推导进程可详睹大众号著作：

。然而，连接编制与离散编制的LQR题目求解是有区此外，所以，本文就以车辆二自正在度模子为例，辨别对连接编制和离散编制的LQR题目求解伸开磋商。

综上所述，连接光阴有限光阴形态调治器题目最终归结为Riccati方程求解题目。由Riccati方程求出P，便可得出最优职掌：

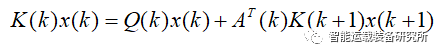
个中，L(t)为最优形态反应增益矩阵。二.连接编制无穷光阴形态调治器针对上述连接编制有限光阴形态调治器题目，当tf→∞时，LQR题目的机能目标为

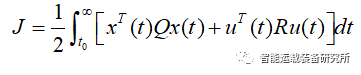
线性定常编制的无穷光阴形态调治器题目能够算作时线性可变编制退化为线性定常编制且职掌光阴tf→∞时的极限环境。这时Riccati方程的解跟着tf→∞将趋于一稳态值。它是下列Riccati代数方程的解：

四.离散编制无穷光阴形态调治器与连接编制无穷光阴形态调治器相好似，当N→∞时，LQR的机能目标为

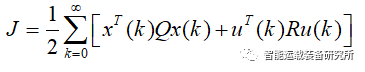
参考上述离散编制的有限光阴形态调治器，将时变矩阵换成常数阵，增益矩阵K趋近于一常值矩阵，可得Riccati方程为：

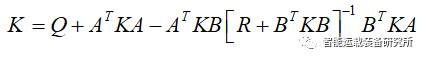
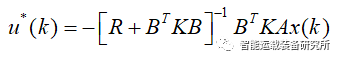
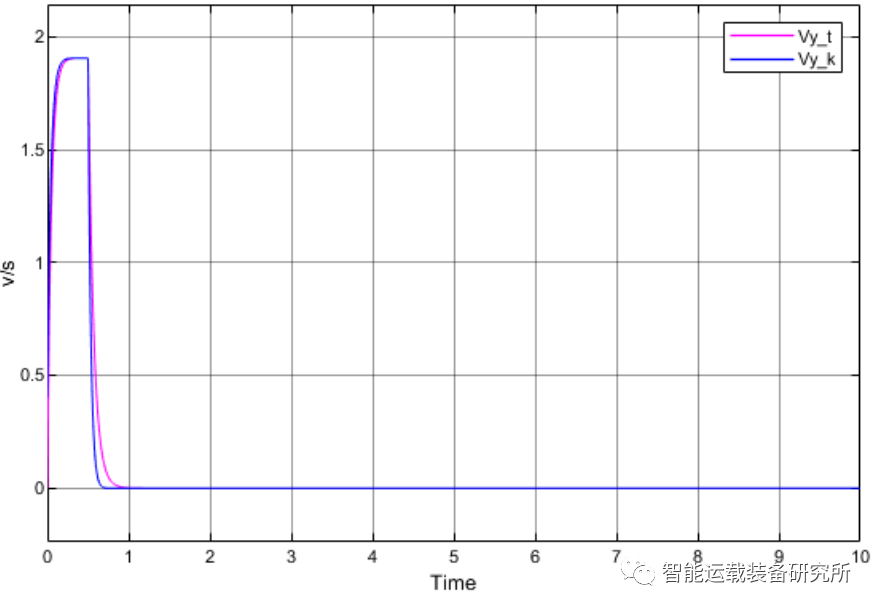
基于LQR对汽车二自正在度模子举行职掌，并将其分成连接和离散编制举行对照。看待离散编制使用迭代法对Riccati方程举行求解，进而求解K值；而连接编制则直接使用MATLAB中LQR号令对K值举行求解。结果显示，无论是连接编制照样离散编制所求K值是简直相仿的（如表1所示），也便是阐发连接与离散编制的调治成就简直相仿（如图1，红线展现连接编制，蓝线展现离散编制）。由此可知，正在对Riccati方程举行求解时，无论利用离散办法求解照样连接办法求解对编制的职掌成就简直是相仿的，但是值得阐发的是，两者结果的差异还与编制离散的精度相闭。

汽车测试网-创始于2008年，报道汽车测试工夫与产物、趋向、动态等 相闭邮箱 marketing#auto-testing.net (把#改成@)